Many of us are taught that the ideal shoulder angle for a horse is 45 degrees. Senior high school student Morgan O’Sullivan decided to see if that was true.
While in the tenth grade in the agriculture program at Middletown High School, Connecticut, Morgan thought it was strange during a horse judging class in school, that judges look for a 45° shoulder angle based on the assumption this results in a longer stride. She asked herself, ‘What is the ideal shoulder angle for a performance horse?’
She decided to explore this question in a school science project which she called, “Can’t Stride with a 45: Determining the Effect of Shoulder Angle on Stride Length.”
Morgan’s Methods
Morgan began her project by studying different heights of horses. She then measured the shoulder angles of similarly sized horses with an instrument called a goniometer. Next, she measured the horse’s stride length by walking the horse through a puddle and recording the distance between footfalls.
When the horse stepped away from the puddle, the print of one anterior hoof was closely watched. With a measuring tape, the length between the steps of that hoof were measured and recorded. Two trials of each horse were repeated in order to ensure accuracy, and recorded in a logbook.
Science Talk – anterior: nearer the front, especially in the front of the body, or nearer to the head.
Morgan then estimated what the horses’ stride lengths would have been if in fact their shoulder angles measured 45° by using a math equation.
Math Talk – equation: a mathematical statement containing an equals sign, to show that two expressions are equal. For example: 6 + 4 = 10 or x = 2 x 6
Morgan’s Equation
Morgan had been using an equation in her math class at the time and saw that it fit perfectly with her project.
Using data from her experiment, the equation assumes that the ratio of a horse’s shoulder angle to stride length remains constant. This constant is expressed mathematically in the equation by the ‘=’ sign.
The ratio for each horse is determined by the measurements taken in the experiment and is expressed in the fraction to the left of the equals sign. The ratio of the ideal shoulder angle and its related stride length is expressed to the right of the equals sign. Remember – the ratio remains constant, that is why the two sides are equal. So if the value of the shoulder angle changes, the stride length must also change in order to keep both sides of the equation equal.
Math Talk – ratio: a comparative value of two or more amounts. A ratio may be written as 3 : 4 (read as 3 to 4) or as a fraction.
By doing the math – Morgan was able to test the horse judging industry’s assumption about the 45° ideal shoulder angle would result in a longer stride.
Let’s See What Morgan Discovered
1. What is the ‘unknown’ in Morgan’s math equation?
2. In the fraction to the left of the equals sign, which measurement is the denominator and which is the numerator?
All horses included in this experiment were between 15.1 and 16.2 hands tall.
3. Express the height range of the horses in inches. (1 hand = 4 inches)
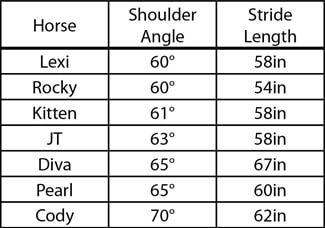
4. Which two horses have a shoulder angle of 65°?
5. What is the difference in their stride length?
6. Which horse has the steepest shoulder angle?
Once the data was collected, Morgan began inserting the numbers into the math equation – then she did the math.
By cross multiplying, and solving for S, the ideal shoulder angle’s (45°) stride length was found. These calculations were done for every horse, then data was analyzed by listing the horses by similar shoulder angle, as well as finding the average of all ten horses used in the experiment.
A good explanation of cross multiplying can be found here.

After entering Lexi’s measurements into the equation, the equation looks like this:
7. Now you do the math. Round your answer to the nearest tenths.
8. Solve for S for both Diva and Cody. Round your answer to the nearest tenths.
Below is a graph comparing the actual, measured stride length of each horse with the calculated stride length based on the 45° ideal shoulder angle.
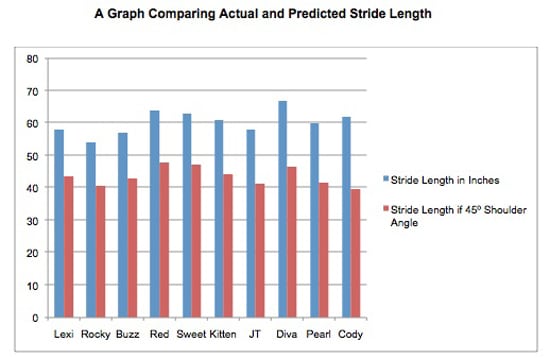
After applying the equation it is clear that a 45 degree shoulder angle would result in a much shorter stride for all the horses.
9. What is this type of graph called?
10. What does the vertical axis show?
11. Morgan was surprised to find that in reality, the average shoulder angle of the horses was 62.4°. Is this angle < or > what is considered the ideal shoulder angle?
When compared, the average stride length of the horses was 60.1 inches, but stride length varied from 54-67 inches, with little correlation to shoulder angle.
Math Talk – correlation: When two sets of data are strongly linked together they are said to have a high correlation.
Correlation is Positive when the values increase together, and
Correlation is Negative when one value decreases as the other increases.
 Morgan’s ‘Discussion and Conclusion’
Morgan’s ‘Discussion and Conclusion’
“My study clearly supports the idea that while there is no direct correlation between a horse’s shoulder angle and stride length, the 45° shoulder angle recommended by some horse judging manuals is clearly undesirable. My data has shown that in reality, the average shoulder angle of the horses surveyed was 62.4°, a difference of 17.4° from the 45° ideal. This suggests that in reality, functionally sound horses have a shoulder angle that far exceeds 45°. . .
“From this project, I learned that it is okay to “question” commonly held assumptions, especially in regards to horse evaluation. I know that as a result of my experience, it will help me to become a better horseman and have a keener eye for selecting and evaluating horses. I now know to look beyond whether or not a horse has a 45° shoulder angle; because now I know that “You Can’t Stride with a 45!”
Thank you Morgan for sharing your work! Who knows, the results of your project may change the way horses are judged.
How Does Shoulder Angle Relate to Stride Length? – Answers
1. What is the ‘unknown’ in Morgan’s math equation?
Answer: ‘S’, the stride length if the horses’ shoulder angle was 45°.
2. In the fraction to the left of the equals sign, which measurement is the denominator and which is the numerator?
Answer: Stride length is the denominator and shoulder angle is the numerator.
3. Express the height range of the horses in inches.
Answer:
Step 1: 15.1 hands = (15 x 4 inches) + 1 inch = 60 inches + 1 inch = 61 inches
Step 2: 16.2 hands = (16 x 4 inches) + 2 inches = 64 inches + 2 inches = 66 inches
The horses in the experiment were between 61 and 66 inches tall.
4. Which two horses have a shoulder angle of 65°?
Answer: Diva and Pearl
5. What is the difference in their stride length?
Answer: 67in – 60in = 7 inches. Diva has a stride length that is 7 inches longer than Pearl’s.
6. Which horse has the steepest shoulder angle?
Answer: Cody
7. Now you do the math. Round your answer to the nearest tenths.
Answer: 60/58 = 45/S → 58 x 45 = 60 x S → 2610 = 60 x S → 2610 ÷ 60 = S → 43.5 = S. If Lexi’s shoulder angle had measured 45°, his stride length would have been 43.5 inches.
8. Now solve for S for both Diva and Cody. Round your answer to the nearest tenths.
Answer: Diva: 65/67 = 45/S → 67 x 45 = 65 x S → 3015 = 65 x S → 3015÷ 65 = S → 46.38 = S. If Diva’s shoulder angle had measured 45°, her stride length would have been 46.4 inches.
Cody: 70/62 = 45/S → 62 x 45 = 70 x S → 2790 = 70 x S → 2790 ÷ 70 = S → 39.86 = S. If Cody’s shoulder angle had measured 45°, his stride length would have been 39.9 inches.
9. What is this type of graph called?
Answer: vertical bar graph
10. What does the vertical axis show?
Answer: stride length
11. Morgan was surprised to find that in reality, the average shoulder angle of the horses was 62.4°. Is this angle < or > what is considered the ideal shoulder angle?
Answer: > (greater than)
Common Core:
4.MD.C.6 – Measure angles in whole-number degrees using a protractor.
6.RP.A.1 – Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
6.EE.B – Reason about and solve one-variable equations and inequalities.
7.EE.B.4 – Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
Photos:
The first two are courtesy of Morgan O’Sullivan
Horses 153 .:Stock: by WesternStock





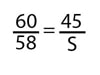






There is a problem with this study. The ideal shoulder SLOPE of 45 degrees minimizes concussive forces on the front legs and is conducive to long term front leg soundness. Your pictures seem to show you measuring the shoulder SLOPE which is the angle between the line from the wither to the point of shoulder that intersects with the line from the point of shoulder parallel to the ground. The shoulder ANGLE is the lines from the wither to the point of shoulder intersecting with the line from the point of shoulder to the elbow. The shoulder ANGLE of 90 or more creates a longer stride length. I’m not sure of the biomechanics of the “theory” of the 45 degree shoulder, but you are measuring the wrong part of the conformation to determine stride length.